Two_Stream_Solution是模块中基于二流近似的辐射传输计算方案，根据介质的optical properties来计算上层的辐射亮度。

辐射传输方程

首先，在平面平行（Plane-parallel）微波在均匀（symmetric）介质中，存在辐射传输方程（radiative transfer equation）如下：
$$
\begin{align}
\mu\frac{dI(\tau,\mu)}{d\tau}=I(\tau,\mu)-\frac{\omega(\tau)}{2}\int_{-1}^1{P_s(\tau,\mu,\mu’)I(\tau,\mu’)d\mu’}-[1-\omega(\tau)]B(T)
\end{align}
$$

首先是公式左边项，也就是辐射传输到$\tau$处的辐亮度变化量。其中，$\tau$可以理解成深度，最顶上等于0，最底层等于1。$\mu=\cos(\theta)$带来的是入射角信息。

公式右边的第一项的实际的$\tau$处的辐亮度。
第二项是散射项，是一种消光作用，所以是负值。$\omega(\tau)$是单次散射反照率（Single Scattering Albedo）,表征的每次散射相对于入射辐射的比值，是$\tau$的函数。
单次散射反照率并非指的是只进行一次散射，相反，散射光还会继续在不同的方向上继续与介质中的散射体发生二次散射，依次类推。但是每次散射都遵循$\omega$这个比值。
散射项中的$\omega*I(\tau,\mu’)$指的是在散射中，散射光的方向是$\mu’=\cos(theta’)$,乘以$\omega$得到对应的强度。对$\cos(\mu’)$从-1->1的积分表示的对全空间的全方位角方向的散射辐射积分。也就是整体散射辐射。
$P_s(\tau,\mu,\mu’)$称为散射相函数，反映的是散射光在空间中的强度情况。在各向同性散射（Isotropic Scattering）中，不同方向的散射强度是相同的。其本质上是一个无穷级数，表示的无限细分的散射方位角，可以进行多项式展开，但是由于是无穷级数，计算机实现起来是不可能的。

$\tau=\sigma_{ext}∆z 和 \omega=\sigma_{sca}/\sigma_{ext}$ 分别来自于Mies散射的计算，后面的章节会介绍到。

第三项是介质的吸收，对应于介质物理温度下的黑体辐射强度$B(T)$,由Planck方程确定

如何计算散射项？
散射相函数$P_s(\tau,\mu,\mu’)$表征的是任意方向的散射分布。一般来说，散射项不可能无限的计算下去，也就是不能对于所有的方向进行散射计算。一般采用的方法是采用离散纵标法（DOM; Discrete Ordinate Method），其思想是只对有限的方向进行离散计算。
比如说应用广泛的32-streams (Tsang and Kong, 1977)近似，提供了足够（sufficient）多的流数。但是这么多级的展开对于是一个很computationally intensive的任务。但是低流数又无法替代多角度的散射，Liou (1992)提出4流比2流有显著的改善，并且计算起来可以接受。
四流近似举例：在Liu et al.,(1998) 中，$P_s(\tau,\mu,\mu’)$ 假设遵循Henyey-Greenstein equation，可以进行Legendre polynomial多项式展开。详细计算过程见Solving RTM using Discrete Ordinate Method (DOM)and How it is implemented in MWRT。
小角度近似？？后向前向？

LandEM中的具体实现

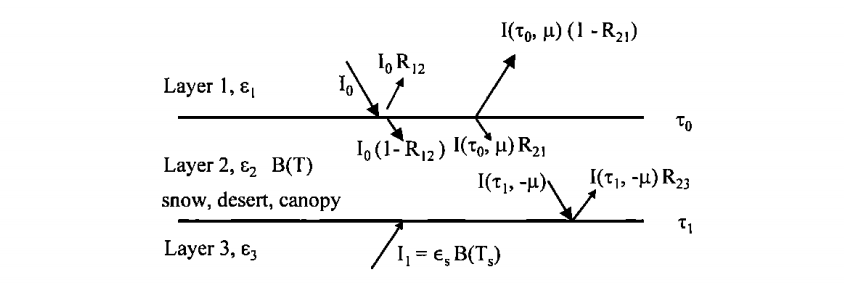
这个代码是在‘土壤-介质-大气’三层模型的基础上进行的二流辐射公式，首先是模型示意图：
土壤-介质-大气近地表模型

代码具体细节：

  • 计算出地表和介质层的截面反射，透射，粗糙表面 – 菲涅尔方程+斯涅耳定律
  • 假设空气和介质之间 $T_{21}=1 ; R_{21}=0$

$$
\begin{align}
\mu &=\cos(\theta) \\
\alpha_h &= \sqrt{\frac{1-\omega_h}{1-g_h*\omega_h}} \\
K_h &=\frac{\sqrt{(1-\omega_h)(1-g_h*\omega_h)}}{\mu} \\
\beta_h &=\frac{1-\alpha_h}{1+\alpha_h} \\
\gamma_h &=\frac{\beta_h - R_{23h}}{1 - \beta_h*R_{23h}} \\
\end{align}
$$

$$
\begin{align}
\alpha_v &= \sqrt{\frac{1-\omega_v}{1-g_v*\omega_v}} \\
K_v &=\frac{\sqrt{(1-\omega_v)(1-g_v*\omega_v)}}{\mu} \\
\beta_v &=\frac{1-\alpha_v}{1+\alpha_v} \\
\gamma_v &=\frac{\beta_v - R_{23v}}{1 - \beta_v*R_{23v}} \\
\end{align}
$$

$$
\begin{align}
fact_1&=\gamma_h*e^{-2K_h*\tau_h} \\
fact_2&=\gamma_v*e^{-2K_v*\tau_v} \\
\end{align}
$$

$$
\begin{align}
gsect_0&=(e^{c^2f/T_{skin}}-1)/(e^{c^2f/T_{soil}}-1) \\
gsect1_h&=(1-R_{23h})*(gsect_0-1) \\
gsect2_h&=\frac{1-\beta_h^2}{1-\beta_h*R_{23h}}*e^{-K_h*\tau_h} \\
\end{align}
$$

$$
\begin{align}
gsect1_v&=(1-R_{23v})*(gsect_0-1) \\
gsect2_v&=\frac{1-\beta_v^2}{1-\beta_v*R_{23v}}*e^{-K_v*\tau_v} \\
\end{align}
$$

$$
\begin{align}
E_h &= T_{21h}*\frac{(1 - \beta_h)*(1 + fact_1)+gsect1_h*gsect2_h}{1-\beta_h*R_{21h}-(\beta_h-R_{21h})*fact_1} \\
E_v &= T_{21v}*\frac{(1 - \beta_v)*(1 + fact_2)+gsect1_v*gsect2_v}{1-\beta_v*R_{21v}-(\beta_v-R_{21v})*fact_2} \\
\end{align}
$$

参考文献：
Tsang, L. and J.A. Kong, 1977: Theory for thermal microwave emission from a bounded medium containing spherical scatters. J. Appl. Phys., 48, 3593-3599.
Liou, K.-N., 1992: Radiation and Cloud Processes in the Atmosphere. Oxford University Press, 487pp.